We will look at the following tests: Runs test, Mann-Whitney U test, Wilcoxon matched-pairs signed ranks test, Kruskal-Wallis test, Friedman test and Spearman’s rank correlation coefficient.
Run’s Test:
Consider a railway station where the station incharge is keeping a tab of whether the train arrives on time on the station or arrives late given that it has arrived on time on the previous station. He needs to find out whether some problems on the track between the previous station and his station is causing the delay of trains or is it random occurrence not attributable to any specific problem.
15 trains arrive on the station in the day. Let the code for arrival on time be 0 and arrival late be 1. also assume that the trains arrive at constants interval. The arrival can be of the form 000000011111111. i.e the first 7 trains arrive on time and the last 8 arrive late. This kind of data can be suspected, why do the trains arriving in the first half of the day come on time and the others don’t. This behaviour coud be non-random. probably, visibility reduces as day progresses and the train driver needs to slow the trains down. Other kind of distribution could be 001011011011000. This kind of distribution could be random. Runs test can be used to establish whether this is indeed random. A run can be defined as an occurrence of a sequence of similar events. For example a 00 in the start of the sequence is one run. The total number of runs are 00-1-0-11-0-11-0-11-000 -> 9.
The Null hypothesis for the run’s test is that the observations in the sample are randomly generated. The alternate hypothesis is that they are not randomly generated. The test differs for small samples and large samples.
Small sample Runs test – for small samples let n1 be the number of observations of event 1 and n2 be the number of observations of event 2. if n1 and n2 are less than or equal to 20 this test can be used. This is how the test is carried out.
1) establish that the small sample test can be used by examining n1 and n2 values.
2) assume a value of alpha (0.05).
3) Use the Runs table for small sample and n1 and n2 and alpha and find out the critical value. Note that the Runs table gives two values. An upper tailed table which gives the higher critical value (C2) and a lower tailed table which gives the lover critical value (C1). if the number of runs (N) of the observation fall within C1 and C2 then the decision is to not reject the null hypothesis. I.e. the sample is indeed random.
Large Sample Run Test:
For n1 and n2 greater than 20 the sampling distribution is normal. The z statistic can be used to check the null hypothesis. The z statistic is given by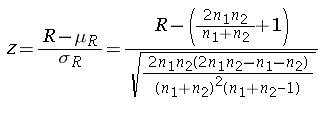
The z table can be used to find out the critical values for the level of alpha. the z values can then be compared. If the z value from the experiment falls outside the critical value from the table, the null hypothesis is rejected. Or if the p-value is less than alpha the null hypothesis is rejected.
Mann-Whitney U Test :
It is a counterpart of the t-test used when the assumption of normal distribution is not valid, or if the data are at least ordinal. The two tailed hypothesis is : Null hypothesis – the populations are identical.
Let us look at this test using an example. Suppose that a researcher wants to find out if the average age of people entering a movie theater is different in two cities.
The example below shows how the Mann-Whitney U test solves the problem.
The steps are:
combine the data and arrange them in ascending order. Assign rank to the observations and also preserve the information about which group the observation comes from. Calculate W1 as the sum of ranks for group 1 elements and W2 as sum of ranks of group 2 elements. Calculate U1 and U2 using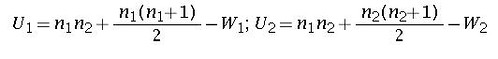
The test statistic is the smaller of the two U values.also note that U1=n1n2-U2. Use that table to calculate the p-value using U (smaller), n1(no of obs for sample having smaller U) and n2. For a two tailed test double the p-value.
For large samples U is approximately normally distributed. A z statistic can be used to check the null hypothesis. The z statistic is given by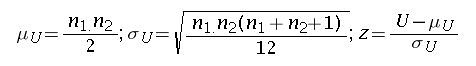
Wilcoxon matched-pairs signed rank test:
The Mann-Whitney test is a t-test counterpart of independent samples. However, if the two sample are related, the wilcoxon matched-pairs signed rank test can be used. This test can be used for situations where the researcher is measuring data before and after studies or data taken from the sample person at two different conditions etc.
The method used for calculation depends on the size of the sample. If the sample is of small size (<15)
here we are comparing the household income for a group of families after a change in government policy. The steps are as follows: first calculate the difference in the income for each pair. Arrange the absolute value of the differences in ascending order and assign ranks to them. For values that have a negative difference change the sign of the rank to negative. Calculate the sum of rank for the negative and positive values. The minimum sum is our test statistic. Compare this value with the value obtained from the T table for given n and alpha. The hypothesis if rejected if the calculated T is less than the T from the table.
Large-Sample Case:
If the sample size is greater than 15 then the T statistic is approximately normally distributed and a z score can be used to check the null hypothesis.
The z formula is given by.
T is calculated in the same way as in small sample size analysis.
Kruskal-Wallis Test:
This test is the non parametric counterpart to one way ANOVA. The parametric ANOVA is based on normally distributed population, independent groups, at least interval level data, and equal population variances. The Kruskal-Wallis test is used to analyse ordinal data and is not based on any assumption of the population distribution. However this test deals with independent populations only and the sample data needs to be selected randomly from the population.
Let the test compare c groups. The null hypothesis is given by
Null Hypothesis – The c population are identical.;Alternate hypothesis : at least one of the c populations is different.
The process is as follows:
1) combine the groups together and arrange the data in ascending order. assign ranks to the data and maintain the group to which the data belongs.
2) In case of a tie between multiple data elements, each tied element is assign the average rank of the tied elements.
3)The K value is calculated as below.
Where c = number of groups
n = total number of items
Tj=total of ranks in a group.
nj=number of items in a group.
4) the K value is compared to the Chi square value with given alpha and df = c-1. If the calculated K value is greater than the chi square value, the null hypothesis is rejected.
5) This is a one tailed test only.
Friedman Test:
This test is the nonparametric counterpart of the randomized block design. Friedman Test can work with populations whose distribution is not known and when data is ranked. The groups need to be independent and the researcher should be able to rank observations in each group .
The null hypothesis is : the populations under treatment are equal.
The alternate hypothesis is : At least on population under the treatment yields larger values than at least one another population under treatment.
Steps for analysis:
1) Rank the data. The ranks are assigned within the group and the data across the group is not combined. see the earlier tests for how data can be ranked. The smallest rank in a group is 1 and the largest is c. c is also the number of treatment levels.
The statistic is calculated using: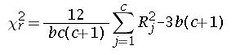
where c = number of treatment levels(columns)
b = number of blocks.(rows)
Rj=total of ranks for a particular treatment level (column)
j=particular treatment level (column)
The value obtained from the formula is compared with the chi square value for given alpha and df=c-1.
Spearman’s Rank Correlation:
The degree of association of two variables when only ordinal level data is available can be calculated from Spearman’s rank correlation given by:
n= number of pairs being correlated.
d = difference in the ranks of each pair.