Chi-Square Goodness of Fit test :
This test is used on experiments that are an extension of binomial distribution, i.e. on multinomial distribution. This distribution has more than two variables or outcomes in an experiment. The chi square compares the observed distribution of outcomes to the expected distribution of outcomes. In other words it shows how well does the observed distribution fit the expected distribution. For example a retail store chain may claim that their customers follow a certain satisfaction distribution as shown below
Satisfied – 80%
Somewhat satisfied – 10%
Not Satisfied – 10%
The results of a random survey undertaken by a particular store manager can be used to test whether the distribution applies to her store as well.
The formula used for the chi-square test is
The chi square distribution is a series of graphs with different values of degrees of freedom.
This is how the test works – Use the chi-square table and the degree of freedom and a suitable alpha value to find the value of chi-square. Use the above formula to calculate the chi-square value for the experiment. If the experimental value is greater than the value of the table then the null hypothesis can be rejected. Note that this is a single tailed test since we are interested in finding out if the observed distribution follows the assumed distribution or not.
Chi-square test of independence : This test can be used to check the distribution of frequencies when there are two variables having different categories. For example if a tyre company wants of find out if the size of tyre used is dependent of the make of the tyre. The response can be obtained on a two way table, for example the test results can be captured with tyre size on the horizontal and tyre make on the vertical. If we have two sizes of tyres and two makes of tyres, we have a 2X2 matrix of results. Each cell containing the frequency for the make-size combination. In a way the chi-square test of independence tells whether the two variables are dependent.
The null hypothesis of the test is that the variables are dependent.
If the variables are dependent the expected frequency of occurrence can be calculated from the experiment using the formula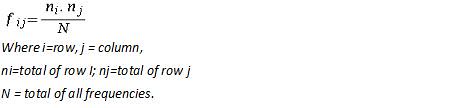
Using this expected values and the observed values, the chi square value can be calculated as